Obliczanie obwodu trójkąta równoramiennego nie musi być trudne. Dzięki prostym wzorom i znajomości długości boków, proces ten staje się przystępniejszy. W naszym artykule znajdziesz wzór na obwód oraz przykłady z różnorodnymi długościami boków. Dodatkowo, zamieściliśmy diagramy, które pomogą lepiej zrozumieć temat.
Jak obliczyć obwód trójkąta równoramiennego?
Aby wyznaczyć obwód trójkąta równoramiennego, sumujemy długości wszystkich jego boków. W takim kształcie dwa boki są identyczne, a trzeci, czyli podstawa, różni się od nich.
Wzór wygląda następująco: O = a + 2b, gdzie a oznacza długość podstawy, a b to długość równych boków[2].
Na przykład, jeśli podstawa mierzy 3 cm, a ramiona po 5 cm, obwód będzie wynosił 13 cm. To proste działanie arytmetyczne pozwala szybko i precyzyjnie określić obwód trójkąta równoramiennego.
Wzór na obwód trójkąta równoramiennego – O = a + 2b
Aby obliczyć obwód trójkąta równoramiennego, stosujemy prosty wzór: O = a + 2b. W tym przypadku a oznacza długość podstawy, natomiast b to długość obu równych boków. Dzięki temu wzorowi łatwo i szybko wyliczymy obwód. Przykładowo, gdy podstawa mierzy 4 cm, a każde z ramion 6 cm, to całkowity obwód będzie równy 16 cm.
Znaczenie długości boków w obliczeniach
Długości boków w trójkącie równoramiennym odgrywają istotną rolę przy precyzyjnym wyznaczaniu obwodu. W takim trójkącie dwie strony są identyczne, a trzecia stanowi podstawę. Wiedza o tych wymiarach umożliwia zastosowanie wzoru: O = a + 2b.
Dzięki symetrii, wynikającej z równych ramion, łatwiej jest analizować jego właściwości[4]. Długość podstawy ma wpływ na kąt między ramionami, co może modyfikować inne obliczenia, takie jak pole trójkąta. W rzeczywistości dokładne określenie wymiarów boków jest kluczowe w budownictwie i projektowaniu, gdzie liczy się precyzja.
Praktyczne przykłady obliczeń obwodu trójkąta równoramiennego
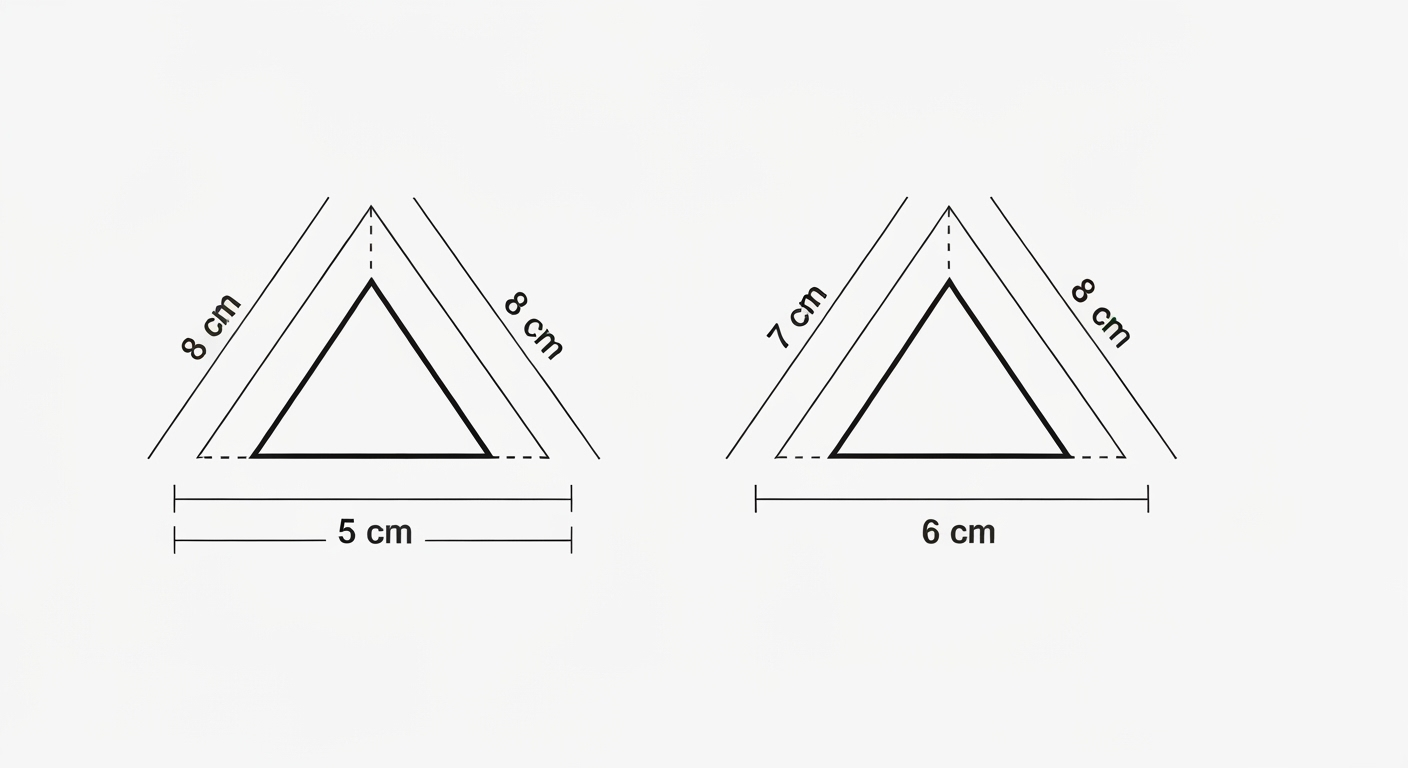
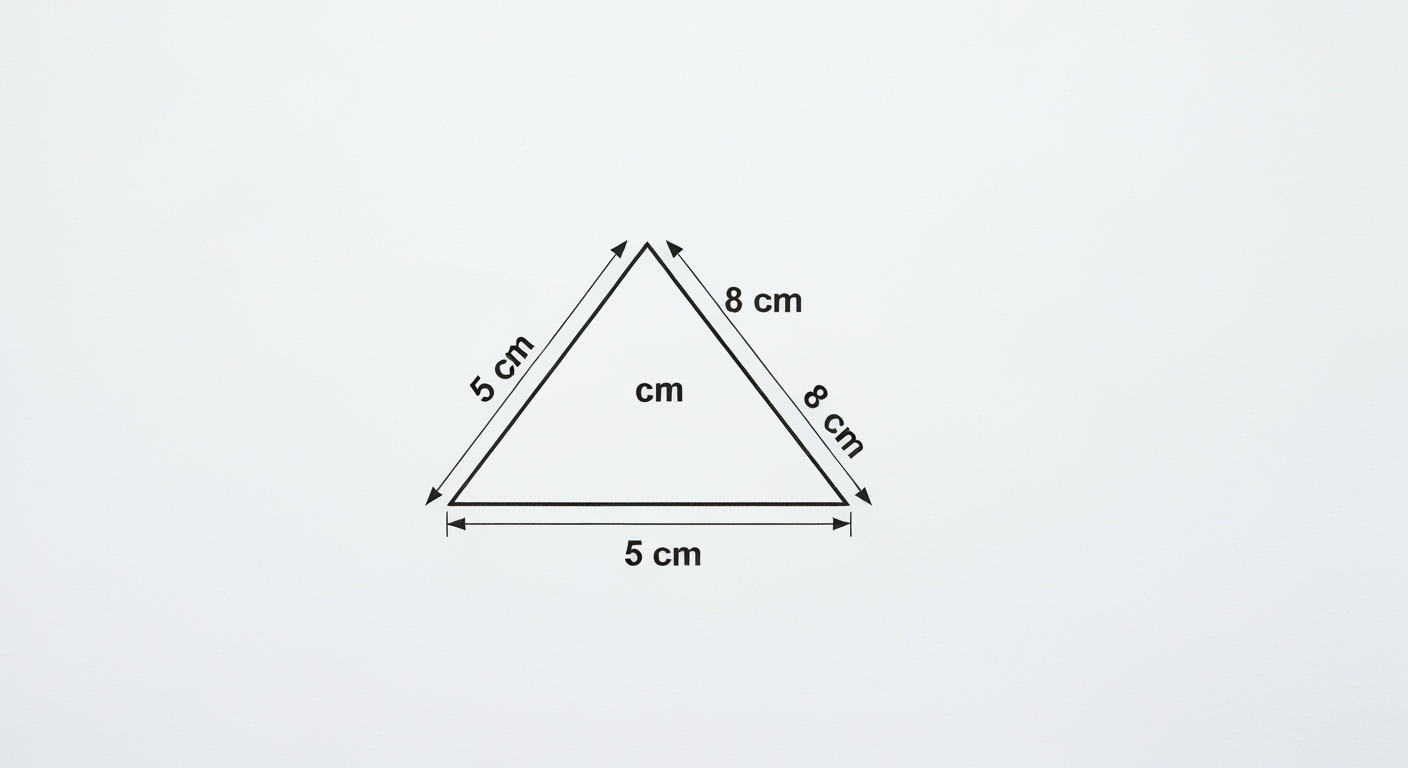
Przykłady obliczania obwodu trójkąta równoramiennego ilustrują zastosowanie wzoru O = a + 2b w różnych kontekstach. Gdy na przykład podstawa trójkąta mierzy 5 cm, a każde z ramion po 8 cm, to obwód wynosi 21 cm. Inna sytuacja: przy podstawie 6 cm i ramionach po 7 cm, otrzymujemy obwód równy 20 cm. Takie przykłady pokazują, jak zmieniające się długości boków wpływają na całkowity obwód. Jest to użyteczne w praktyce, np. w projektowaniu lub budownictwie. Dodatkowo, obliczanie obwodu w różnych jednostkach, takich jak centymetry czy metry, pozwala na dopasowanie wyników do specyficznych wymagań.
Przykłady z różnymi długościami boków
Przyjrzyjmy się kilku przykładom, które ukazują, jak różnorodne długości boków mogą oddziaływać na obwód trójkąta równoramiennego. Wyobraźmy sobie trójkąt, w którym podstawa mierzy 5 cm, a ramiona mają długość po 9 cm. W takim przypadku obwód wynosi 23 cm. Z kolei, jeśli podstawa ma 7 cm, a ramiona po 8 cm, również otrzymujemy obwód równy 23 cm.
Te sytuacje doskonale obrazują, jak obwody trójkątów mogą się różnić przy zmiennych długościach boków, co jest kluczowe w projektowaniu i budowaniu konstrukcji[6].
Diagramy trójkąta równoramiennego dla lepszego zrozumienia
Diagramy trójkąta równoramiennego stanowią istotny element w poznawaniu jego struktury oraz symetrii. Dzięki nim łatwiej zauważyć, w jaki sposób długości boków wpływają na obwód tej figury[7].
Traktując trójkąt jako płaszczyznę, diagramy pozwalają lepiej przyswoić wzór O = a + 2b, gdzie a to podstawa, a b to równe ramiona. Taka wizualizacja ułatwia również zrozumienie kątów, co jest niezwykle przydatne przy analizowaniu jego właściwości, takich jak proporcje i kąty.
Diagramy znajdują zastosowanie nie tylko w edukacji, ale także w praktycznych dziedzinach, takich jak:
- projektowanie,
- budownictwo,
- gdzie precyzyjne pomiary są niezwykle ważne.
Źródła:
- [1] https://parenting.pl/obwod-trojkata-jak-go-policzyc/6956329748994560a
- [2] https://matmag.pl/klasa/5/video/oblicz-obwod-trojkata
- [3] https://szaloneliczby.pl/obwod-trojkata/
- [4] https://bazywiedzy.com/trojkat-rownoramienny.html
- [5] https://www.naukowiec.org/wiedza/matematyka/obwod-trojkata_3109.html
- [6] https://prostir.pl/jak-obliczyc-obwod-trojkata/
- [7] https://matematicus.pl/wzor-na-pole-i-obwod-trojkata/

Dzień dobry, nazywam się Krystyna Kownacka i jestem nauczycielem dyplomowanym. Nauczam w przedszkolu oraz w szkole średniej. Zapraszam na mojego bloga.